TALES

 Tales de Mileto

Biografía

Vivió y murió en Mileto, polis griega de la costa Jonia (hoy en Turquía). Fue el iniciador de la Escuela de Mileto a la que pertenecieron también Anaximandro (su discípulo) y Anaxímenes (discípulo del anterior). En la antigüedad se le consideraba uno de los Siete Sabios de Grecia. No se conserva ningún texto suyo y es probable que no dejara ningún escrito a su muerte. Desde el siglo V a. C. se le atribuyen importantes aportaciones en el terreno de la filosofía, la matemática, la astronomía, la física, etc., así como un activo papel como legislador en su ciudad natal.

A menudo Tales es considerado el iniciador de la especulación científica y filosófica griega y occidental, aunque su figura y aportaciones están rodeadas de grandes incertidumbres.

Se suele aceptar que Tales comenzó a usar el pensamiento deductivo aplicado a la geometría, y se le atribuye la enunciación de dos teoremas geométricos que llevan su nombre.

                             

Teorema de Tales

Existen dos teoremas relacionados con la geometría clásica que reciben el nombre de teorema de Tales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a.C.

Primer Teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

                                  

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

Segundo Teorema

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo.

 
                                        

Aportes Matemáticos.

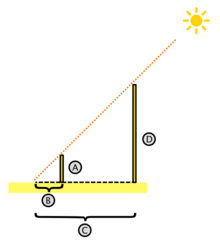
Es muy conocida la leyenda acerca de un método de comparación de sombras que Tales habría utilizado para medir la altura de las pirámides egipcias: el milesio se percató de que se podría saber la altura exacta de las pirámides midiendo la sombra de estas en el momento del día en que su sombra era más o menos de igual tamaño que su cuerpo. Este método fue aplicado luego a otros fines prácticos de la navegación. Se supone además que Tales conocía ya muchas de las bases de la geometría, como el hecho de que cualquier diámetro de un círculo lo dividiría en partes idénticas, que un triángulo isósceles tiene por fuerza dos ángulos iguales en su base o las propiedades relacionales entre los ángulos que se forman al cortar dos paralelas por una línea recta perpendicular.

                                         

Información sacada de: 

• Wikipedia
• biografiasyvidas
• Google Imágenes