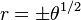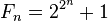FERMAT
Biografía
(Beaumont, Francia, 1601 - Castres, id., 1665) Matemático francés. Continuador de la obra de Diofanto en el campo de
los números enteros y cofundador del estudio matemático de la
probabilidad, junto con Pascal, y de la geometría analítica, junto con
Descartes, Pierre de Fermat mantuvo correspondencia con los grandes
científicos de su época y gozó ya en vida de gran estima e inmensa
reputación, si bien su natural modestia y su modo de trabajar, en exceso
diletante, perjudicó la divulgación de sus aportaciones.
La existencia de este ilustre matemático fue ciertamente sencilla y
prosaica, y se conoce poco de sus primeros años. Hijo de Dominique
Fermat, burgués y segundo cónsul de Beaumont, estudió leyes en Toulouse y
quizá en Burdeos para poder aspirar al ejercicio de la magistratura;
llegado, en efecto, a consejero del Parlamento de la ciudad de Toulouse,
fue progresando allí en su labor lenta y tranquilamente,
distinguiéndose por su probidad, su tacto y sus corteses maneras.
Interesado por las matemáticas, consagró a ellas su
tiempo de ocio, y hacia 1637 figuraba entre los principales cultivadores
europeos de esta ciencia. Hizo amistad con el matemático Carcavi, quien
le relacionó con el padre Marin Marsenne,
amigo de todos los doctos franceses de la época. El padre Mersenne le
puso en contacto con Roberval y con el gran René Descartes (1637).
El trato con el difícil e inquieto genio de
Descartes no resultaba fácil para nadie, ni tampoco lo fue para Pierre
de Fermat, a pesar de su discreción: ambos discutieron sobre cuestiones
científicas (la infracción de la luz y el método de los máximos y
mínimos). Fueron necesarias la mediación de Roberval y toda la prudencia
de Fermat para mantener por lo menos fríamente correctas las relaciones
personales entre los dos sabios. Muy viva, en cambio, fue la amistad
entre Fermat y otro gran matemático de la época, Blaise Pascal; ambos se
conocieron también gracias a Carcavi.
De talante modesto, Pierre de Fermat sólo llego a dar a la imprenta su monografía Dissertatio geometrica de linearum curvarum comparatione,
e hizo públicos algunos de sus mayores descubrimientos sólo por medio
de breves comunicaciones verbales y epistolares. Ello bastó para darlo a
conocer como uno de los grandes matemáticos del momento, pero sus
deberes profesionales y su particular forma de trabajar redujeron en
gran medida el impacto de su obra, extremadamente prolífica. Tenía por
ejemplo la costumbre de anotar, en los márgenes de los libros que leía,
sus ideas y sus descubrimientos, desgraciadamente sin sus
demostraciones, por falta de espacio. Superando no pocas dificultades,
sus escritos fueron publicados póstumamente por su hijo Samuel en 1679,
en un volumen titulado Varia opera matemática D. Petri de Fermat: Senatoris Tolosani.

Obra
Espiral de Fermat
También conocida como espiral parabólica, es una curva que responde a la siguiente ecuación en coordenadas polares:
Es un caso particular de la espiral de Arquímedes.
Números amigos
Dos números amigos son dos números naturales a y b tales que a es la suma de los divisores propios de b, y b es la suma de los divisores propios de a. (La unidad se considera divisor propio, pero no lo es el mismo número.)
En 1636, Fermat descubrió que 17.296 y 18.416 eran una pareja de
números amigos, además de redescubrir una fórmula general para
calcularlos, conocida por Tabit Ibn Qurra alrededor del año 850.
Números primos
Un número de Fermat es un número natural de la forma:
donde n es natural.
Pierre de Fermat conjeturó que todos los números naturales de esta forma con n natural eran números primos, pero Leonhard Euler probó que no era así en 1732. En efecto, al tomar n=5 se obtiene un número compuesto:
Teorema sobre la suma de dos cuadrados
El teorema sobre la suma de dos cuadrados afirma que todo número primo p, tal que p-1 es divisible entre 4, se puede escribir como suma de dos cuadrados. El 2 también se incluye, ya que 12+12=2. Fermat anunció su teorema en una carta a Marin Mersenne fechada el 25 de diciembre de 1640, razón por la cual se le conoce también como Teorema de navidad de Fermat.
Pequeño teorema de Fermat
El pequeño teorema de Fermat, referente a la divisibilidad de números, afirma que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p, siendo p un número primo. Su interés principal está en su aplicación al problema de la primalidad y en criptografía.
El Último Teorema de Fermat
El último teorema de Fermat, conjeturado por Pierre de Fermat en 1637, pero no demostrado, establece que:
si n es un número entero mayor que 2, entonces no existen números enteros no nulos x, y y z, tales que se cumpla la igualdad:
He sacado la información de:
- biografiasyvidas
- Google Imágenes
- Wikipedia
- http://matematicascercanas.com