SOFÍA KOWALEVSKY

SOFÍA KOWALEVSKY

Biografía

(Sofía Vasílievna Kovalevskaya o Kovaliévskaia; Moscú, 1850 - Estocolmo, 1891) Fue la primera matemática rusa de importancia y la primera mujer que consiguió una plaza de profesora universitaria en Europa (Suecia, 1881). Nacida y criada en el seno de una familia gitana rusa de buena formación académica. Sofía, era también descendiente de Matías Corvino, rey de Hungría. Su abuelo, por casarse con una gitana y estar emparentado con dicha etnia, perdió el título hereditario de príncipe.

Vivió su infancia en Palibino, Bielorrusia. Sofia amaba desde niña la lectura y la poesía, se sentía poeta en su interior. Además de su hermana, dos de sus tíos influyeron notablemente en su vida. Uno de ellos, un auténtico amante de la lectura y aunque no era matemático le apasionaba esta ciencia; su otro tío le enseñaba ciencias y biología. A menudo se sentaba en un banco del patio para ver mecerse con el oleaje, provocado por el viento, la pelota del estanque quedándose sumergida en sus pensamientos matemáticos.

Bajo la guía del tutor de su familia, Y. I. Malevich, Sofía comenzó sus primeros estudios reales de matemáticas. A los trece años empezó a mostrar muy buenas cualidades para el álgebra. Por esa época escribió: «Comencé a sentir una atracción tan intensa por las matemáticas, que empecé a descuidar mis otros estudios». Pero su padre, a quien le horrorizaban las mujeres sabias, decidió interrumpir las clases de matemáticas de su hija. Aun así Sofia siguió estudiando por su cuenta con libros de álgebra. Pidió prestado un ejemplar del Álgebra de Bourdeu que leía a la noche cuando el resto de la familia dormía. Así, aquello que nunca había estudiado lo fue deduciendo poco a poco. Un año más tarde un vecino, el Profesor Tyrtov, presentó a la familia de Sofía un libro del que él era autor y Sofía trató de leerlo. No entendió las fórmulas trigonométricas e intentó explicárselas a sí misma.

Sofia, a partir de los conocimientos que ya tenía, explicó y analizó por sí misma lo que era el concepto de seno tal y como había sido inventado originalmente. Un profesor descubrió las facultades de Sofia, y habló con su padre para recomendarle que facilitara los estudios a su hija. Al cabo de varios años su padre accedió y Sofia comenzó a tomar clases particulares.

Los años de su adolescencia fueron años de rebelión, la época de las grandes revoluciones y manifestaciones de siglo XIX en las que el socialismo feminista iba perdiendo terreno. Su apellido de soltera era Korbin-Kukóvzkaya y era descendiente de un rey de Polonia. A los once años se enamora del escritor F. D., exnovio de su hermana. Más tarde, al casarse, adopta el apellido del marido.

Kovalevskaya murió de gripe a los cuarenta y un años, luego de un viaje de placer a Génova. Sus restos descansan en Suecia.

Doctorado

Al mismo tiempo que estudiaba, comenzaba su trabajo de doctorado. Durante sus años en Berlín escribió tres tesis: dos sobre temas de matemáticas y una tercera sobre astronomía. Más tarde el primero de estos trabajos apareció en una publicación matemática a la que contribuían las mentes más privilegiadas.

Obras

Entre sus trabajos figuran: Sobre la teoría de las ecuaciones diferenciales, que aparece en el Journal de Crelle, y Sobre la rotación de un cuerpo sólido alrededor de un punto fijo, por el cual obtiene un importante premio otorgado por la Academia de Ciencias de París, en 1888.

El teorema de Cauchy-Kovalévskaya formaba parte del trabajo por el que obtuvo el doctorado. Fue publicado en Crelle´s Journal. Es un teorema de existencia y unicidad de soluciones de una ecuación en derivadas parciales de orden k con condiciones iniciales para funciones analíticas. En 1842 Cauchy había demostrado la existencia de solución de una ecuación en derivadas parciales lineales de primer orden. En la misma época, Weierstrass, que no conocía los trabajos de Cauchy, demostró la existencia y "unicidad" de la solución para un sistema de ecuaciones diferenciales ordinarias y propone a Sonia extender estos resultados a un sistema de ecuaciones en derivadas parciales. Este teorema, elaborado independientemente del de Cauchy, generaliza sus resultados y establece unas demostraciones tan simples, completas y elegantes que son las que se exponen en la actualidad en los libros de Análisis.

Posiblemente la investigación más importante fue la que realizó sobre la rotación de un cuerpo sólido alrededor de un punto fijo por la que recibió el Premio Bordin de la Academia de Ciencias de París y más tarde el premio de la Academia de Ciencias de Suecia. Ambos trabajos fueron publicados en el Acta Mathematica. Una de las aplicaciones más importantes de la mecánica newtoniana es el estudio del movimiento de un cuerpo. Leonhard Euler (1758) había resuelto el problema cuando el punto respecto al que gira es el centro de gravedad. J. L. Lagrange (1811-1815), el de un cuerpo de revolución que gira alrededor de un eje. Pero estaba sin resolver el caso general. La Academia de Ciencias de Prusia había propuesto este problema para un concurso los años 1855 y 1858, pero nadie se había presentado. Sofia resolvió de forma analítica las ecuaciones del movimiento. Planteó un sistema de seis ecuaciones diferenciales, consideró el tiempo como una variable compleja y analizó los casos en los que las seis funciones implicadas, las tres componentes del vector velocidad angular y las tres del vector unitario vertical (aceleración de la gravedad), eran funciones meromorfas del tiempo, con este planteamiento los movimientos estudiados por Euler y Lagrange eran casos particulares, además encontró un tercer caso y lo estudió. Con ello este problema quedaba analíticamente resuelto.

 

 

Honores

Entre otros honores póstumos, el cráter lunar Kovalevskaya lleva su nombre y la Fundación Alexander Von Humboldt de Alemania entrega el premio Sofia Kovalevskaya a los investigadores jóvenes más prometedores.

 

 

 He sacado la información de:

• Wikipedia

• divulgamat2

• Google Imágenes

• mujeresparapensar

SOPHIE GERMAIN

SOPHIE GERMAIN

Biografía

Matemática francesa. Nació el 1 de abril de 1776 en París.

Hija de Ambroise-Francoise Germain, que llegó a ser presidente del Banco de París.

Vivió en una era de preconceptos y chovinismo, y para realizar sus investigaciones se vio obligada a asumir una identidad falsa, estudiar en condiciones terribles y trabajar en aislamiento intelectual.

Al no poder asistir a la escuela porque no aceptaban mujeres, se las arreglaba para recibir apuntes de los profesores. Se inscribió en la Escuela Politécnica de París con el nombre de un antiguo alumno de la misma y algunos profesores de gran relevancia se fijaron en este alumno y aunque pronto descubrieron su verdadero sexo, la protegieron.

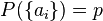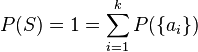En 1801, comunicó al matemático alemán Carl Gauss, unos resultados que le parecían interesantes sobre teoría de números, y nuevamente firmó M. LeBlanc, estudiante de l' Ecole Polytechnique; a partir de entonces estableció con Gauss una correspondencia regular. En 1816, siendo ya muy apreciada en los círculos matemáticos, alcanzó la celebridad al obtener el premio propuesto por la Academia de las Ciencias sobre la teoría de las superficies elásticas, cuestión sometida ya tres veces a concurso y quedando hasta entonces desierto. Realizó descubrimientos importantes en teoría de números, en física matemática, acústica y elasticidad.

Sophie Germain iba a recibir el título de Doctor Honoris Causa de la Universidad de Gottingen en la que trabajaba Gauss, pero murió un mes antes de la fecha, el 26 de Junio de 1831 en París debido a un cáncer de mama.

 

Teorema de Sophie Germain

 El teorema de Sophie Germain dice que si n es un número primo y 2n+1 también es primo, entonces el primer caso del teorema de Fermat es verdadero (cuando ninguno de los tres números es divisible por n). A esos números terminaron llamándoles números primos de Sophie Germain y forman una sucesión 2, 3, 5, 11, 23,28,...

Teoría de la elasticidad 

Descubrir las ecuaciones diferenciales de las superficies vibrantes parecía demasiado difícil a los ojos de la mayor parte de los matemáticos. A pesar de las lagunas de su formación, o quizás por ello, Sophie fue la única concursante. Lo tomó como un reto, y el 21 de septiembre de 1811 presentó una memoria a la Academia, pero su trabajo fue considerado incompleto e incorrecto, y el jurado decidió posponer dos años más el premio. Lagrange corrigió el análisis matemático y obtuvo, a partir de la hipótesis de Sophie, la base para describir el comportamiento estático y dinámico de las placas en puntos del interior.

En esta memoria y por analogía con los trabajos de Euler en el caso unidimensional de la cuerda vibrante, Sophie postula que “en un punto de la superficie la fuerza de elasticidad es proporcional a la suma de las curvaturas principales de la superficie en dicho punto”, que es lo que siempre llamará “mi hipótesis”. A partir de una supuesta relación de equilibrio y utilizando varias hipótesis sobre los desplazamientos y rotaciones de la placa obtenía una ecuación en derivadas parciales de sexto orden en la que buscaba soluciones regulares, en casos particulares, mediante series trigonométricas.

Aunque, en efecto, varios puntos de su trabajo son discutibles, la idea de que la suma de las curvaturas principales en una superficie tiene el mismo papel que la curvatura en el caso unidimensional de la cuerda vibrante es original. Además Sophie no se desalentó sino que, animada de que Lagrange hubiera utilizado con éxito su idea, siguió trabajando con el objetivo de justificar su hipótesis con consideraciones geométricas sobre la deformación de un plano y comparando sus cálculos con las experiencias de Chladni y con otras muchas que realizó ella misma. En 1813 presentó la segunda memoria, por la que obtuvo una mención de honor ya que sus deducciones teóricas explicaban los resultados experimentales.

En 1814 Poisson redactó un trabajo sobre el mismo asunto que leyó el día 1 de agosto de ese mismo año, ante los componentes de la Primera Clase del Instituto de Francia, de la que formaba parte. Comenzó criticando el enfoque de los trabajos anteriores sobre este tema de Leonhard Euler, Jacques Bernouilli y por último de la memoria anónima que el año anterior había recibido una mención de honor. Poisson era discípulo de Laplace y compartía con él la teoría “molecular” que intentaba explicar todos los fenómenos físicos con el modelo de la física newtoniana, es decir, por un conjunto de fuerzas atractivas o repulsivas. Desde este punto de vista, considerando el equilibrio de una sola molécula de la superficie elástica, obtuvo una ecuación, horrible, no lineal y además falsa, que por simplificaciones “milagrosas” se convertía en la ecuación de la segunda memoria de Sophie que, en ese momento, había ganado credibilidad. No la publicó, supuestamente, para no influir en el concurso que había sido convocado de nuevo, pero apareció un resumen de la misma en el “Bulletin de la Societé Philomatique” y en la “Correspondence de l'Ecole Polytecnique”. Sophie, que no tuvo acceso a ella y sólo pudo leer dicho resumen, en un principio se desalentó pero, más tarde, saber que Poisson había llegado a la misma ecuación que ella, le animó a continuar sus investigaciones y presentó otro estudio en 1815.

Este tercer trabajo: “Mémoire sur les Vibrations des Surfaces Élastiques”, por el que se le concedió, al fin, el premio extraordinario de la Academia, suponía una defensa de la legitimidad de su hipótesis a la vez que un ataque al modelo laplaciano y a la teoría molecular. También, en ella, se proponía matematizar el concepto de forma de una superficie y el de deformación. Planteaba que, considerando en un punto dado, la suma de las curvaturas relativas a todas las curvas producidas por las diferentes secciones de la superficie que pasan por la normal se obtendría una expresión que matematizaba la forma de la superficie en un punto. Por lo tanto estaba proponiendo, implícitamente, un procedimiento integral para definir la curvatura en el espacio... Además establecía que esta suma infinita se reducía a las dos curvaturas principales, es decir, las curvaturas máxima y mínima.

En 1821 la publicó, por cuenta propia, con el título “Recherches sur la théorie des surfaces élastiques” posiblemente con objeto de pasar a la posteridad, que ningún colega se apropiara de sus investigaciones, o a causa de su rivalidad con Poisson, que en su trabajo de 1814 había utilizado los resultados de su segunda memoria.

En 1826 publicó “Remarques ...” y en 1828 “Examen des Principes …”. En estas dos memorias sus objetivos son, además de una intervención implícita en la polémica suscitada entre Poisson y Navier sobre la teoría de la elasticidad, replantear su trabajo y, sobre todo, su enfoque, radicalmente opuesto al paradigma molecular y en particular al de Poisson.

He sacado la información de:

• buscabiografias.com
• Google Imágenes
• matemolivares
• divulgamat2

LAPLACE

LAPLACE

Biografía

(Pierre-Simon, marqués de Laplace; Beaumont-en-Auge, Francia, 1749 - París, 1827) Matemático francés. Hijo de un granjero, inició sus estudios primarios en la escuela local, pero gracias a la intervención de D'Alembert, quien había quedado profundamente impresionado por un escrito del joven sobre los principios de la mecánica, pudo trasladarse a la capital, donde consiguió una plaza en la École Militaire. 

Entre 1771 y 1789 desarrolló la mayor parte de su trabajo sobre astronomía, particularmente su estudio sobre las desigualdades planetarias, seguido por algunos escritos sobre cálculo integral y ecuaciones diferenciales en derivadas parciales. Destaca entre su producción del período 1784-1787 la determinación de la atracción de un esferoide sobre una partícula situada en su exterior, para cuya determinación introduciría el análisis de armónicos o coeficientes de Laplace y el concepto de potencial. 

En 1796 publicó su Exposición del sistema del mundo, en el que ofreció una versión divulgativa de las leyes de Newton y una exposición del sistema solar. Sus resultados analíticos sobre la mecánica estelar se publicaron en los cinco volúmenes del Tratado de mecánica celeste (1799-1825). En los dos primeros volúmenes describió métodos para el cálculo del movimiento de los planetas y sus satélites, y determinó sus trayectorias. El tercero contiene la aplicación de estos métodos y muchas tablas astronómicas.

En 1814, Laplace publicó un ensayo sobre probabilidades orientado al lector profano, que le serviría de base para la segunda introducción de su Teoría analítica de las probabilidades (tratado publicado en 1812), donde incluyó una exposición del método de los mínimos cuadrados, base de toda la teoría de los errores.

Obra

• Exposition du systeme du monde (1796)
  En esta obra se presenta, de forma resumida, la historia de la astronomía. Se suele considerar este texto como una de las obras maestras de la literatura en su idioma y procura a su autor el honor de entrar en la Academia Francesa en 1816.Demuestra que los movimientos planetarios son estables y que las perturbaciones producidas por la influencia mutua de los planetas o por cuerpos externos, como los cometas, solamente son temporales. Trata de dar una teoría racional del origen del Sistema Solar en su hipótesis nebular de la evolución estelar.
  
  
• Traite de mecanique celeste (1799-1825) con el Tratado de Mecánica Celeste, monumental obra en 5 volúmenes publicados entre 1799 y 1825, se culmina el trabajo de más de un siglo de duración durante el cual los científicos intentarón dar una explicación matemática de la teoría de la gravitación universal basada en los principios de Newton.
  
• Théorie Analytique des Probabilités (1812) Con la Teoría Analítica de las Probabilidades, expone los principios y las aplicaciones de lo que él llama "geometría del azar". Esta obra representa la introducción de los recursos del análisis matemático en el estudio de los fenómenos aleatorios y recopila toda una serie de memorias publicadas desde 1771.

• Ensayo filosófico sobre el fundamento de las probabilidades (1814) Laplace pretende que esta esta obra represente respecto a la Teoría Analítica de las Probabilidades lo que ha significado Exposición del Sistema del Mundo respecto a Mecáncia Celeste. Es decir, dar a conocer los principios y aplicaciones de la geometría del azar pero sin aparato matemático alguno.
  

Modelo de Laplace 

Su definición nos dice que:

sea E un experimento cualquiera y S el conjunto finito de sus resultados posibles tal que ,

si suponemos que cada resultado es equiprobable (que ninguno tenga más oportunidades que otro), entonces .

Si queremos que P sea una función de probabilidad tal que entonces .

Sea A un subconjunto de S tal que entonces

Transformada de Laplace

La transformada de Laplace es un tipo de transformada integral frecuentemente usada para la resolución de ecuaciones diferenciales ordinarias. La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:

siempre y cuando la integral esté definida. Cuando f(t) no es una función, sino una distribución con una singularidad en 0, la definición es

Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:

La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).
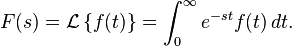
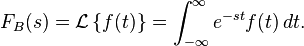
es llamado el operador de la transformada de Laplace.

He buscado información en:

• Google Imágenes
• biografiasyvidas
• estadisticaparatodos.es
• Wikipedia

CAUCHY

CAUCHY

Biografía

(París, 1789-Sceaux, Francia, 1857) Matemático francés. Era el mayor de los seis hijos de un abogado católico y realista, que hubo de retirarse a Arcueil cuando estalló la Revolución. Allí sobrevivieron de forma precaria, por lo que Cauchy creció desnutrido y débil. 

Fue educado en casa por su padre y no ingresó en la escuela hasta los trece años, aunque pronto empezó a ganar premios académicos. A los dieciséis entró en la École Polytechnique parisina y a los dieciocho asistía a una escuela de ingeniería civil, donde se graduó tres años después. 

Su primer trabajo fue como ingeniero militar para Napoleón, ayudando a construir las defensas en Cherburgo. A los veinticuatro años volvió a París y dos más tarde demostró una conjetura de Fermat que había superado a Euler y Gauss. 

Con veintisiete años ya era uno de los matemáticos de mayor prestigio y empezó a trabajar en las funciones de variable compleja, publicando las 300 páginas de esa investigación once años después. En esta época publicó sus trabajos sobre límites, continuidad y sobre la convergencia de las series infinitas. En 1830 se exilió en Turín, donde trabajó como profesor de física matemática hasta que regresó a París (1838). Pasó el resto de su vida enseñando en La Sorbona. 

Publicó un total de 789 trabajos, entre los que se encuentran el concepto de límite, los criterios de convergencia las fórmulas y los teoremas de integración y las ecuaciones diferenciales de Cauchy-Riemann. Su extensa obra introdujo y consolidó el concepto fundamental de rigor matemático.

 

                                 

Obra

En 1814 publicó la memoria de la integral definida que llegó a ser la base de la teoría de las funciones complejas. Gracias a Cauchy, el análisis infinitesimal adquiere bases sólidas.

Cauchy precisa los conceptos de función, de límite y de continuidad en la forma actual o casi actual, tomando el concepto de límite como punto de partida del análisis y eliminando de la idea de función toda referencia a una expresión formal, algebraica o no, para fundarla sobre la noción de correspondencia. Los conceptos aritméticos otorgan ahora rigor a los fundamentos del análisis, hasta entonces apoyados en una intuición geométrica que quedará eliminada, en especial cuando más tarde sufre un rudo golpe al demostrarse que hay funciones continuas sin derivadas, es decir: curvas sin tangente.

 Teorema de Cauchy (teoría de grupos)

El Teorema de Cauchy es un caso particular de los Teoremas de Sylow. Afirma que para todo grupo finito G, si existe un primo p que divide al orden del grupo (donde el orden del grupo es el número de elementos de G), entonces existe un elemento a de G que tiene orden p (donde el orden de a es el menor entero positivo k tal que a^k = e, siendo e el elemento unidad de G)

 Reconocimientos

• 1832: Miembro de la Royal Society
• 1845: Miembro de la Royal Society of Edinburgh
• Es uno de los 72 científicos cuyo nombre figura inscrito en la Torre Eiffel.
• Existe un cráter lunar con su nombre: el cráter Cauchy.

 He sacado la información de:

• Google Imágenes
• biografiasyvidas
• Wikipedia