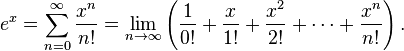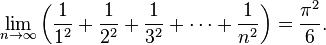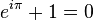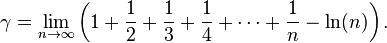TMIMAT1607: marzo 2016

LEONHARD EULER

Biografía

(Basilea, Suiza, 1707 - San Petersburgo, 1783) Matemático suizo. Las facultades que desde temprana edad demostró para las matemáticas pronto le ganaron la estima del patriarca de los Bernoulli, Johann, uno de los más eminentes matemáticos de su tiempo y profesor de Euler en la Universidad de Basilea. Tras graduarse en dicha institución en 1723, cuatro años más tarde fue invitado personalmente por Catalina I para convertirse en asociado de la Academia de Ciencias de San Petersburgo, donde coincidió con otro miembro de la familia Bernoulli, Daniel, a quien en 1733 relevó en la cátedra de matemáticas.

A causa de su extrema dedicación al trabajo, dos años más tarde perdió la visión del ojo derecho, hecho que no afectó ni a la calidad ni al número de sus hallazgos. Hasta 1741, año en que por invitación de Federico el Grande se trasladó a la Academia de Berlín, refinó los métodos y las formas del cálculo integral (no sólo gracias a resultados novedosos, sino también a un cambio en los habituales métodos de demostración geométricos, que sustituyó por métodos algebraicos), que convirtió en una herramienta de fácil aplicación a problemas de física. Con ello configuró en buena parte las matemáticas aplicadas de la centuria siguiente (a las que contribuiría luego con otros resultados destacados en el campo de la teoría de las ecuaciones diferenciales lineales), además de desarrollar la teoría de las funciones trigonométricas y logarítmicas (introduciendo de paso la notación e para definir la base de los logaritmos naturales).

En 1748 publicó la obra Introductio in analysim infinitorum, en la que expuso el concepto de función en el marco del análisis matemático, campo en el que así mismo contribuyó de forma decisiva con resultados como el teorema sobre las funciones homogéneas y la teoría de la convergencia. En el ámbito de la geometría desarrolló conceptos básicos como los del ortocentro, el circuncentro y el baricentro de un triángulo, y revolucionó el tratamiento de las funciones trigonométricas al adoptar ratios numéricos y relacionarlos con los números complejos mediante la denominada identidad de Euler; a él se debe la moderna tendencia a representar cuestiones matemáticas y físicas en términos aritméticos.

En el terreno del álgebra obtuvo así mismo resultados destacados, como el de la reducción de una ecuación cúbica a una bicuadrada y el de la determinación de la constante que lleva su nombre. A lo largo de sus innumerables obras, tratados y publicaciones introdujo gran número de nuevas técnicas y contribuyó sustancialmente a la moderna notación matemática de conceptos como función, suma de los divisores de un número y expresión del número imaginario raíz de menos uno. También se ocupó de la teoría de números, campo en el cual su mayor aportación fue la ley de la reciprocidad cuadrática, enunciada en 1783.

A raíz de ciertas tensiones con su patrón Federico el Grande, regresó nuevamente a Rusia en 1766, donde al poco de llegar perdió la visión del otro ojo. A pesar de ello, su memoria privilegiada y su prodigiosa capacidad para el tratamiento computacional de los problemas le permitieron continuar su actividad científica; así, entre 1768 y 1772 escribió sus Lettres à une princesse d'Allemagne, en las que expuso concisa y claramente los principios básicos de la mecánica, la óptica, la acústica y la astrofísica de su tiempo.

De sus trabajos sobre mecánica destacan, entre los dedicados a la mecánica de fluidos, la formulación de las ecuaciones que rigen su movimiento y su estudio sobre la presión de una corriente líquida, y, en relación a la mecánica celeste, el desarrollo de una solución parcial al problema de los tres cuerpos -resultado de su interés por perfeccionar la teoría del movimiento lunar-, así como la determinación precisa del centro de las órbitas elípticas planetarias, que identificó con el centro de la masa solar. Tras su muerte, se inició un ambicioso proyecto para publicar la totalidad de su obra científica, compuesta por más de ochocientos tratados, lo cual lo convierte en el matemático más prolífico de la historia.

Image result for leonhard euler biografia

Obra

Euler trabajó prácticamente en todos los ámbitos de las matemáticas: geometría, cálculo, trigonometría, álgebra, teoría de números, además de física continua, teoría lunar y otras áreas de la física. Adicionalmente, hizo aportaciones relevantes a la lógica matemática con su diagrama de conjuntos.
Ha sido uno de los matemáticos más prolíficos de la historia. Su actividad de publicación fue incesante (un promedio de 800 páginas de artículos al año en su época de mayor producción, entre 1727 y 1783), y una buena parte de su obra completa está sin publicar. La labor de recopilación y publicación completa de sus trabajos, llamados Opera Omnia,comenzó en 1911 y hasta la fecha ha llegado a publicar 76 volúmenes. El proyecto inicial planeaba el trabajo sobre 887 títulos en 72 volúmenes. Se le considera el ser humano con mayor número de trabajos y artículos en cualquier campo del saber, sólo equiparable a Gauss. Si se imprimiesen todos sus trabajos, muchos de los cuales son de una importancia fundamental, ocuparían entre 60 y 80 volúmenes. Además, y según el matemático Hanspeter Kraft, presidente de la Comisión Euler de la Universidad de Basilea, no se ha estudiado más de un 10% de sus escritos. Por todo ello, el nombre de Euler está asociado a un gran número de cuestiones matemáticas.

Se cree que fue el que dio origen al pasatiempos Sudoku creando una serie de pautas para el cálculo de probabilidades.

Notación matemática

Euler introdujo y popularizó varias convenciones referentes a la notación en los escritos matemáticos en sus numerosos y muy utilizados libros de texto. Posiblemente lo más notable fue la introducción del concepto de función matemática, siendo el primero en escribir f(x) para hacer referencia a la función f aplicada sobre el argumento x. Esta nueva forma de notación ofrecía más comodidad frente a los rudimentarios métodos del cálculo infinitesimal existentes hasta la fecha, iniciados por Newton y Leibniz, pero desarrollados basándose en las matemáticas del último.

También introdujo la notación moderna de las funciones trigonométricas, la letra e como base del logaritmo natural o neperiano (el número e es conocido también como el número de Euler), la letra griega Σ como símbolo de los sumatorios y la letra

i

para hacer referencia a la unidad imaginaria. El uso de la letra griega π para hacer referencia al cociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.

El número e

Euler definió la constante matemática conocida como número

e

como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función

f(x)

=

e

^x en el punto

x=0

es exactamente 1. Es más, es el número real tal que la función

f(x)

=

e

^x se tiene como derivada a sí misma. La función

e

^x es también llamada función exponencial y su función inversa es el logaritmo neperiano, también llamado logaritmo natural o logaritmo en base

e

.

El número

e

puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, una fracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, tiene como forma el límite: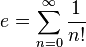

e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n, e=\lim_{n\to 0}\left(1+n\right)^\frac{1}{n}

y también la serie:

e=\sum_{n=0}^\infty \frac{1}{n!}

Además, Euler es muy conocido por su análisis y su frecuente utilización de la serie de potencias, es decir, la expresión de funciones como una suma infinita de términos como la siguiente:

e^x = \sum_{n=0}^\infty {x^n \over n!} = \lim_{n \to \infty}\left(\frac{1}{0!} + \frac{x}{1!} + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!}\right).

Uno de los famosos logros de Euler fue el descubrimiento de la expansión de series de potencias de la función arcotangente. Su atrevido, aunque, según los estándares modernos, técnicamente incorrecto uso de las series de potencias le permitieron resolver el famoso problema de Basilea en 1735, por el cual quedaba demostrado que:

\lim_{n \to \infty}\left(\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots + \frac{1}{n^2}\right) = \frac{\pi ^2}{6}.

Euler introdujo el uso de la función exponencial y de los logaritmos en las demostraciones analíticas. Descubrió formas para expresar varias funciones logarítmicas utilizando series de potencias, y definió con éxito logaritmos para números negativos y complejos, expandiendo enormemente el ámbito de la aplicación matemática de los logaritmos. También definió la función exponencial para números complejos, y descubrió su relación con las funciones trigonométricas. Para cualquier número real φ, la fórmula de Euler establece que la función exponencial compleja puede establecerse mediante la siguiente fórmula:

e^{i\varphi} = \cos \varphi + i\sin \varphi.\,

Siendo un caso especial de la fórmula (cuando

\varphi

\pi

), lo que se conoce como la identidad de Euler:

e^{i \pi} +1 = 0 \,

Esta fórmula fue calificada por Richard Feynman como «la fórmula más reseñable en matemáticas», porque relaciona las principales operaciones algebraicas con las importantes constantes 0, 1,

e

i

y π, mediante la relación binaria más importante.En 1988, los lectores de la revista especializada The Mathematical Intelligencer votaron la fórmula como «la más bella fórmula matemática de la historia». En total, Euler fue el responsable del descubrimiento de tres de las cinco primeras fórmulas del resultado de la encuesta.

Además de eso, Euler elaboró la teoría de las funciones trascendentes (aquellas que no se basan en operaciones algebraicas) mediante la introducción de la función gamma, e introdujo un nuevo método para resolver ecuaciones de cuarto grado. También descubrió una forma para calcular integrales con límites complejos, en lo que sería en adelante el moderno análisis complejo, e inventó el cálculo de variaciones incluyendo dentro de su estudio a las que serían llamadas las ecuaciones de Euler-Lagrange.

Euler también fue pionero en el uso de métodos analíticos para resolver problemas teóricos de carácter numérico. Con ello, Euler unió dos ramas separadas de las matemáticas para crear un nuevo campo de estudio, la teoría analítica de números. Para ello, Euler creó la teoría de las series hipergeométricas, las series q, las funciones hiperbólicas trigonométricas y la teoría analítica de fracciones continuas. Por ejemplo, demostró que la cantidad de números primos es infinita utilizando la divergencia de series armónicas, y utilizó métodos analíticos para conseguir una mayor información sobre cómo los números primos se distribuyen dentro de la sucesión de números naturales. El trabajo de Euler en esta área llevaría al desarrollo del teorema de los números primos.

Matemática aplicada

Algunos de los mayores éxitos de Euler fueron en la resolución de problemas del mundo real a través del análisis matemático, en lo que se conoce como matemática aplicada, y en la descripción de numerosas aplicaciones de los números de Bernoulli, las series de Fourier, los diagramas de Venn, el número de Euler, las constantes e y π, las fracciones continuas y las integrales. Integró el cálculo diferencial de Leibniz con el método de fluxión de Newton, y desarrolló herramientas que hacían más fácil la aplicación del cálculo a los problemas físicos. Euler ya empleaba las series de Fourier antes de que el mismo Fourier las descubriera y las ecuaciones de Lagrange del cálculo variacional, las ecuaciones de Euler-Lagrange.

Hizo grandes avances en la mejora de las aproximaciones numéricas para resolver integrales, inventando lo que se conoce como las aproximaciones de Euler. Las más notables de estas aproximaciones son el método de Euler para resolver ecuaciones diferenciales ordinarias, y la fórmula de Euler-Maclaurin. Este método consiste en ir incrementando paso a paso la variable independiente y hallando la siguiente imagen con la derivada. También facilitó el uso de ecuaciones diferenciales, en particular mediante la introducción de la constante de Euler-Mascheroni:

\gamma = \lim_{n \rightarrow \infty } \left( 1+ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{n} - \ln(n) \right).

Por otro lado, uno de los intereses más llamativos de Euler fue la aplicación de las ideas matemáticas sobre la música. En 1739 escribió su obra Tentamen novae theoriae musicae, esperando con ello poder incorporar el uso de las matemáticas a la teoría musical. Esta parte de su trabajo, sin embargo, no atrajo demasiada atención del público, y llegó a ser descrita como demasiado matemática para los músicos y demasiado musical para los matemáticos.

Reconocimientos y honores

Euler es conmemorado por la Iglesia Luterana en su Calendario de Santos el 24 de mayo, en su condición de devoto cristiano (creyente en la infalibilidad de la Biblia) y de apologista convencido contrario al ateísmo creciente de su época.
Varias calles de ciudades de todo el mundo llevan su nombre, como sucede en París (Francia), Basilea (Suiza), Binzen (Alemania), México, D.F. (México), Buenos Aires (Argentina), Padua (Italia) o Englewood (Estados Unidos).
En conmemoración suya, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos.
Numerosos sellos postales tanto suizos como alemanes y rusos llevan su efigie.
El cŕater lunar Euler recibió ese nombre en su honor.
El asteroide (2002) Euler también debe su nombre al gran matemático.

Image result for leonhard euler billetes y sellos

He sacado la información de:

Wikipedia
biografiasyvidas
Google Imágenes

jueves, 17 de marzo de 2016

EULER

El número e

Matemática aplicada