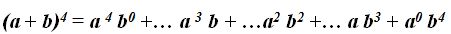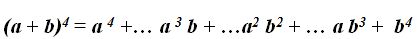DESCARTES

DESCARTES

Biografía

(La Haye, Francia, 1596 - Estocolmo, Suecia, 1650)

René Descartes se educó en el colegio jesuita de La Flèche (1604-1612), por entonces uno de los más prestigiosos de Europa, donde gozó de un cierto trato de favor en atención a su delicada salud. Los estudios que en tal centro llevó a cabo tuvieron una importancia decisiva en su formación intelectual; conocida la turbulenta juventud de Descartes, sin duda en La Flèche debió cimentarse la base de su cultura. Las huellas de tal educación se manifiestan objetiva y acusadamente en toda la ideología filosófica del sabio.

El programa de estudios propio de aquel colegio (según diversos testimonios, entre los que figura el del mismo Descartes) era muy variado: giraba esencialmente en torno a la tradicional enseñanza de las artes liberales, a la cual se añadían nociones de teología y ejercicios prácticos útiles para la vida de los futuros gentilhombres. Aun cuando el programa propiamente dicho debía de resultar más bien ligero y orientado en sentido esencialmente práctico (no se pretendía formar sabios, sino hombres preparados para las elevadas misiones políticas a que su rango les permitía aspirar), los alumnos más activos o curiosos podían completarlos por su cuenta mediante lecturas personales. 

Años después, Descartes criticaría amargamente la educación recibida. Es perfectamente posible, sin embargo, que su descontento al respecto proceda no tanto de consideraciones filosóficas como de la natural reacción de un adolescente que durante tantos años estuvo sometido a una disciplina, y de la sensación de inutilidad de todo lo aprendido en relación con sus posibles ocupaciones futuras (burocracia o milicia). Tras su etapa en La Flèche, Descartes obtuvo el título de bachiller y de licenciado en derecho por la facultad de Poitiers (1616), y a los veintidós años partió hacia los Países Bajos, donde sirvió como soldado en el ejército de Mauricio de Nassau. En 1619 se enroló en las filas del duque de Baviera. 

Según relataría el propio Descartes en el Discurso del Método, durante el crudo invierno de ese año se halló bloqueado en una localidad del Alto Danubio, posiblemente cerca de Ulm; allí permaneció encerrado al lado de una estufa y lejos de cualquier relación social, sin más compañía que la de sus pensamientos. En tal lugar, y tras una fuerte crisis de escepticismo, se le revelaron las bases sobre las cuales edificaría su sistema filosófico: el método matemático y el principio del cogito, ergo sum. Víctima de una febril excitación, durante la noche del 10 de noviembre de 1619 tuvo tres sueños, en cuyo transcurso intuyó su método y conoció su profunda vocación de consagrar su vida a la ciencia. 

Tras renunciar a la vida militar, Descartes viajó por Alemania y los Países Bajos y regresó a Francia en 1622, para vender sus posesiones y asegurarse así una vida independiente; pasó una temporada en Italia (1623-1625) y se afincó luego en París, donde se relacionó con la mayoría de científicos de la época.

En 1628 decidió instalarse en Holanda, país en el que las investigaciones científicas gozaban de gran consideración y, además, se veían favorecidas por una relativa libertad de pensamiento. Descartes consideró que era el lugar más favorable para cumplir los objetivos filosóficos y científicos que se había fijado, y residió allí hasta 1649. 

Los cinco primeros años los dedicó principalmente a elaborar su propio sistema del mundo y su concepción del hombre y del cuerpo humano. En 1633 debía de tener ya muy avanzada la redacción de un amplio texto de metafísica y física titulado Tratado sobre la luz; sin embargo, la noticia de la condena de Galileo le asustó, puesto que también Descartes sostenía en aquella obra el movimiento de la Tierra, opinión que no creía censurable desde el punto de vista teológico. Como temía que tal texto pudiera contener teorías condenables, renunció a su publicación, que tendría lugar póstumamente. 

En 1637 apareció su famoso Discurso del método, presentado como prólogo a tres ensayos científicos. Por la audacia y novedad de los conceptos, la genialidad de los descubrimientos y el ímpetu de las ideas, el libro bastó para dar a su autor una inmediata y merecida fama, pero también por ello mismo provocó un diluvio de polémicas, que en adelante harían fatigosa y aun peligrosa su vida.

                                

 Obras

Aunque se conservan algunos apuntes de su juventud, la primera obra de Descartes fue Reglas para la dirección del espíritu, escrita en 1628, aunque quedó inconclusa, y que se publicó póstumamente en 1701. Luego Descartes escribió El mundo o tratado de la luz y El hombre, que retiró de la imprenta al enterarse de la condena de la Inquisición a Galileo en 1633, y que más tarde se publicaron a instancias de Gottfried Leibniz. En 1637 publicó el Discurso del método para dirigir bien la razón y hallar la verdad en las ciencias, seguido de tres ensayos científicos: La Geometría, Dióptrica y Los meteoros. Con estas obras, escritas en francés, Descartes acaba por presentarse ante el mundo erudito, aunque inicialmente intentó conservar el anonimato.

En 1641 publicó las Meditaciones metafísicas, acompañadas de un conjunto de Objeciones y respuestas que amplió y volvió a publicar en 1642. Hacia 1642 puede fecharse también el diálogo, obra póstuma, La búsqueda de la verdad mediante la razón natural.

En 1644 aparecen los Principios de filosofía, que Descartes idealmente habría planeado para la enseñanza. En 1649 publicó un último tratado, Las pasiones del alma, sin embargo aún pudo diseñar para Cristina de Suecia el reglamento de una sociedad científica, cuyo único artículo es que el turno de la palabra corresponda rotativamente a cada uno de los miembros, en un orden arbitrario y fijo.

 Filosofía

Al menos desde que Hegel escribió sus Lecciones de historia de la filosofía, en general se considera a Descartes como el padre de la filosofía moderna, independientemente de sus muy relevantes aportes a las matemáticas y la física. Este juicio se justifica, principalmente, por su decisión de rechazar las verdades recibidas, p. ej., de la escolástica, combatiendo activamente los prejuicios. Y también, por haber centrado su estudio en el propio problema del conocimiento, como un rodeo necesario para llegar a ver claro en otros temas de mayor importancia intrínseca: la moral, la medicina y la mecánica. En esta prioridad que concede a los problemas epistemológicos, lo seguirán todos sus principales sucesores. Por otro lado, los principales filósofos que lo sucedieron estudiaron con profundo interés sus teorías, sea para desarrollar sus resultados o para objetarlo. Este es el caso de Pascal, Spinoza, Newton, Leibniz, Malebranche, Locke, Hume y Kant, cuando menos. Sin embargo, esta manera de juzgarlo no debe impedirnos valorar el conocimiento y los estrechos vínculos que este autor mantiene con los filósofos clásicos, principalmente con Platón y Aristóteles, pero también Cicerón y Sexto Empírico. Descartes aspira a «establecer algo firme y duradero en las ciencias». Con ese objeto, según la parte tercera del Discurso, por un lado él cree que en general conviene proponerse metas realistas y actuar resueltamente, pero prevé que en lo cotidiano, así sea provisionalmente, tendrá que adaptarse a su entorno, sin lo cual su vida se llenará de conflictos que lo privarán de las condiciones mínimas para investigar. Por otra parte, compara su situación a la de un caminante extraviado, y así concluye que en la investigación, libremente elegida, le conviene seguir un rumbo determinado. Esto implica atenerse a una regla relativamente fija, un método, sin abandonarla «por razones débiles»...

Metafísica

Otra postura que Descartes sostiene es la evidencia de la libertad. Pero más que discutir la realidad o no del libre albedrío, Descartes parece partir de la hipótesis de que él mismo es libre para poner esta libertad en práctica: ya la investigación, en su caso, resulta de una determinación voluntaria y libre. Además, la epistemología cartesiana, vg., su investigación sobre las condiciones de validez del conocimiento, hace un aporte tácito, pero fundamental, al campo de la filosofía práctica: la responsabilidad no es ilusoria, pues si hay conocimiento legítimo, y éste versa en parte sobre algunas relaciones causales, hemos de tomar nuestras decisiones sin dar oídos sordos a las consecuencias previsibles de nuestros actos.

Sin embargo, parece que Descartes nunca intentó demostrar la corrección de la citada hipótesis sobre el libre albedrío, como no fuera poniéndola a prueba indirectamente, acaso examinando su capacidad de producir resultados favorables. Descartes compara el cuerpo de los conocimientos a un árbol cuyas raíces son de tipo metafísico, el tronco equivale a la física, y las ramas principales son las artes mecánicas, cuya importancia está en que permiten disminuir el trabajo de los hombres, la medicina y la moral. La metafísica es fundamental, pero añade que los frutos de un árbol no se cogen de las raíces, sino de las ramas.

 Las reglas del método

Tras el hundimiento de la filosofía aristotélico-tomista, el ob­jetivo fundamental de Descartes es encontrar un método que, partiendo de una serie de reglas, garantice el razona­miento correcto y la reconstrucción de todo el saber huma­no. Las reglas de dicho método son las siguientes:

1)   Regla de la evidencia, que exige rechazar cualquier idea que no sea clara (es decir, indudable) y distinta (imposi­ble de confundir con ninguna otra). Se llega a la eviden­cia, bien por intuición, o visión intelectual directa de una verdad (como los primeros principios del razona­miento), bien por deducción, que permite derivar una serie de consecuencias necesariamente ciertas de tales principios intuitivamente evidentes.

2)   Regla del análisis, que consiste en reducir lo complejo a sus componentes más simples, que pueden conocerse in­tuitivamente.

3)   Regla de la síntesis, por la cual, partiendo de los elemen­tos simples, conocidos por intuición, se construyen argu­mentos o deducciones más complejas.

4)   Regla de la enumeración, en cuya aplicación se revisan todos los pasos dados para comprobar que no se han co­metido errores en el razonamiento.

 Duda metórica

La duda metódica es el método de Descartes para descubrir verdades ciertas. En general, se opone a la duda escéptica en que la duda metódica tiene un carácter constructivo y provisional, mientras que la duda escéptica suele ser más destructiva y permanente.

La duda metódica consiste, hablando en términos muy generales, en dudar de todas las verdades adquiridas por cualquier vía hasta llegar a alguna que se muestre tan evidente por sí misma que haga imposible la duda. Siguiendo este método fue como Descartes llegó a afirmar, con toda seguridad eso de “pienso, luego existo”.

Sobre la base de esta verdad, “pienso, luego existo”, Descartes construyó toda su filosofía. Esta tiene un doble sentido. Por un lado, en el transcurso de la duda, Descartes se da cuenta de que no puede dudar de que está dudando, puesto dudar de que se duda es dudar, así que sabe con toda seguridad que duda. Ahora bien, dado que dudar es pensar, entonces no puedo dudar que pienso. El hecho de que pienso, indica la existencia de un ser pensante, pues los pensamientos necesitan este soporte. Así que Descartes llega a esta verdad cierta: puesto que hay pensamiento, hay una cosa que piensa.

Ahora bien, el proceso que lleva a Descartes a descubrir que hay una cosa que piensa tiene una dirección inequívoca. En efecto, va desde el acto de pensar a la existencia de una cosa que piensa, porque es a partir de este acto que se deduce la existencia de la cosa que piensa. De otro modo, la cosa que piensa tiene una existencia dudosa, es decir, que podría existir de hecho, aunque nosotros no lo podríamos saber con toda seguridad, de modo que sin el acto de pensar, que lleva a la cosa que piensa, no se cumpliría el requisito de imposibilidad de toda duda impuesto por Descartes. Así, la premisa incuestionable es: “hay pensamiento” y su conclusión: “hay algo que piensa”.

De este modo sembraba Descartes la semilla del idealismo moderno, el cual daría una prioridad lógica, epistemológica y ontológica al sujeto.

 He sacado la información de:

• biografiasyvidas
• Wikipedia
• Google Imágenes
• iesdionisioaguado
• filosofia.laguia2000.com

CARDANO

CARDANO

Biografía

(Jérôme Cardan; Pavía, actual Italia, 1501 - Roma, 1576) Matemático italiano. Se graduó en la Universidad de Pavía y se doctoró en medicina (1526) en la de Padua. En 1536 se trasladó a Milán, donde empezó a ejercer como profesor de matemáticas.

En 1539 publicó su primera obra en dicha materia, la Práctica de matemáticas y mediciones individuales, en la que recogió el contenido de sus clases. Ese mismo año fue admitido en la facultad de medicina, de la que al poco fue nombrado rector. En 1543, ya con una sólida fama como médico (a él se debe la primera descripción clínica de la fiebre tifoidea), se trasladó de nuevo a Pavía.

Dos años después publicó su obra científica más importante, el Ars magna, donde se recoge un exhaustivo estudio de las ecuaciones de tercer grado o cúbicas, y en la que se ofrece la regla para la resolución de las mismas que lleva su nombre. Por la publicación de dicho resultado fue duramente criticado por el también matemático Niccolò Tartaglia, quien se lo había revelado con la condición de que lo mantuviera en secreto y no lo divulgara, si bien Cardano, al descubrir otra fuente en la que se contenía dicha regla, se creyó liberado de su promesa. 

Otras obras suyas de importancia fueron el Libro sobre juegos y azar, en el cual ofreció la primera aproximación sistemática a la teoría de la probabilidad y enunció la ley de los grandes números, resultados todos ellos que no serían abordados de nuevo (por Blaise Pascal y Pierre de Fermat) hasta un siglo más tarde. Publicó asimismo títulos de contenido filosófico, como La sutileza de las cosas, que fueron muy leídos en su tiempo. 

Los últimos años de su vida estuvieron plagados de desgracias, desde la ejecución en el año 1560 de uno de sus hijos, acusado de asesinato, hasta un proceso por herejía por el que llegó a ser encarcelado (1570). Absuelto un año después, pero privado del derecho de publicar obra alguna, se trasladó a Roma ciudad en la que redactó su autobiografía Mi propia vida, que concluyó poco antes de su muerte.

Obra

Como médico en la medicina renacentista ha sido estudiado agudamente por N. Siraisi, en The Clock and the Mirror. Fue Cardano el primero en describir la fiebre tifoidea y sobre otros temas médicos, como comentarios a Galeno e Hipócrates. Su Contradicentium medicorum, de 1536, aborda temas de discusión en la medicina del siglo XVI. Su El libro de los sueños es la última onirocrítica de raíces antiguas (que culminó con Artemidoro en el siglo II) y medievales, pasada por el filtro crítico de los modernos, lo que lo hace un texto valiosísimo; sería citado por Freud en su Interpretación de los sueños (1900).

Hoy es conocido por sus múltiples intereses, pese a la lentitud de la recuperación en lenguas vivas (ya que escribió en latín). Son fuentes de datos las dos enciclopedias de saberes: De subtilitate rerum (1550) y De varietate rerum (1559).

 

                                                   

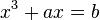En primer lugar, destaca por sus trabajos de álgebra. En 1539 publicó su libro de aritmética Practica arithmetica et mensurandi singulares. Publicó las soluciones a las ecuaciones de tercer y cuarto grado en su Ars magna datado en 1545. La solución a un caso particular de ecuación cúbica (en notación moderna), le fue comunicada a través de Niccolò Fontana (más conocido como Tartaglia) a quien Cardano había jurado no desvelar el secreto de la resolución; no obstante, Cardano consideró que el juramento había expirado tras obtener información de otras fuentes por lo que polemizó con Tartaglia, a quien además cita. En realidad, el hallazgo de la solución de las ecuaciones cúbicas no se debe ni a Cardano ni a Tartaglia (había hallado una primera fórmula Scipione dal Ferro hacia 1515) y hoy se reconoce la honradez de Cardano que lo reconocía así en su libro. Una ecuación de cuarto grado fue resuelta por un discípulo de Cardano llamado Lodovico Ferrari. En su exposición, puso de manifiesto lo que hoy se conoce como números imaginarios.

Su libro sobre juegos de azar, Liber de ludo aleae, escrito en la década de 1560 pero publicado póstumamente en 1663, constituye el primer tratado serio de probabilidad abordando métodos de cierta efectividad.

Hizo Cardano contribuciones a la hidrodinámica, apoyándose en esquemas del siglo XV, y mantuvo que el movimiento perpetuo es imposible excepto en los cuerpos celestes. Publicó dos enciclopedias de ciencias naturales, Sobre la sutileza de las cosas, Sobre la variedad de las cosas, que contienen una amplia variedad de invenciones, hechos y conocimientos que hoy consideramos mágicos o supersticiosos. También introdujo la rejilla de Cardano, una herramienta criptográfica, en 1550. Asimismo desarrolló un dispositivo que permite conservar la horizontalidad mediante dos ejes que giran en ángulo, dispositivo que actualmente se usa en millones de vehículos, conocido hoy como junta o suspensión de cardano y otro para el asentamiento de las brújulas en las naves llamado gimbal.

En filosofía —que ha sido estudiado a fondo por A. Ingegno, Saggio sulla filosofia di Cardano— no sólo escribió sobre temas morales (De consolatione, De sapientia, Proxeneta), pues en De immortalitate animorum Cardanó reabrió una discusión que había tenido lugar años antes entre Pietro Pomponazzi, Agostino Nifo, Alessandro Achillini y Marcantonio Zimara, principalmente. Ellos habían discutido, en el seno de las tradiciones filosóficas de Aristóteles y Averroes, cuáles habían sido sus posturas, y qué podía decir la razón natural sobre la inmortalidad del hombre. Cardano se significó en oposición a Pietro Pomponazzi, seguidor de Alejandro de Afrodisias.

Sus dos libros biográficos, Mi vida, y Mis libros (su autobibliografía) son dos obras maestras, que hacen además un retrato excelente de lo que pudo ser un sabio, como era, del siglo XVI, y la valoración de sus libros.

Su Opera omnia se publicó en Lyon en el siglo XVII, y ha tenido una ed. facsímil en el siglo XX (hay microforma de la Univ. de Valencia ISBN 978-84-370-1887-4). El trabajo de recuperación prosigue desde Milán en la actualidad.

He sacado la información de:

• Wikipedia
• Google Imágenes
• biografiasyvidas

TARTAGLIA

TARTAGLIA

Biografía

(Brescia, actual Italia, 1499 - Venecia, 1557) (Niccolo Fontana) Matemático italiano. Durante la ocupación francesa de Brescia su padre fue asesinado y él mismo dado por muerto a causa de sus graves heridas, una de las cuales, un golpe de sable en la mandíbula, le provocaría un defecto en el habla que lo acompañaría toda su vida y le valdría su sobrenombre (tartaglia, esto es, tartamudo). De origen muy humilde, su familia no pudo proporcionarle ningún tipo de educación, de modo que el joven Tartaglia tuvo que aprenderlo todo por su cuenta. Ya adulto, se ganó la vida como profesor itinerante (según permiten conocer sus obras, vivió en Verona, Mantua y Venecia) y a través de su participación en concursos matemáticos. En uno de ellos se planteó la resolución de diversas ecuaciones de la forma x³ + px = q; Tartaglia consiguió averiguar la solución general y obtuvo el premio. Más adelante reveló su método a Gerolamo Cardano, bajo la firme promesa de mantener el secreto, pero éste acabó publicándolo en su Ars magna de 1545.

Después de que Gerolamo Cardano rompiera su promesa de mantener en secreto su resolución de las ecuaciones de tercer grado, Tartaglia se decidió a publicar la importante obra Problemas e invenciones varias (1546), cuyos cuatro primeros libros se refieren a la balística y al arte militar, el quinto a la topografía, y los tres siguientes a las fortificaciones y a la estática; muy interesante resulta el noveno, que trata del álgebra y de la resolución de las ecuaciones de tercer grado y de los problemas correspondientes. La parte dedicada al arte de la fortificación fue la que atrajo más la atención de sus contemporáneos: a consecuencia de la invención de la pólvora pírica, el arte de la guerra había experimentado profundas transformaciones que hacían necesarios nuevos medios de ofensiva, y un estudio que sirviese para aumentar su potencia y la precisión en relación con la nueva técnica de fortificar.

Tartaglia destaca asimismo en los estudios de matemáticas por su traducción italiana de los Elementos de Euclides (1543) y por la de De insidentibus aquae de Arquímedes; de esta última obra publicó además un amplio comentario con paráfrasis, que utilizó posteriormente en La invención elaborada (1551), donde se trata del sistema adecuado para llevar nuevamente a flote las naves hundidas.

 Obras

La obra más extensa de Tartaglia es el incompleto Tratado general de números y medidas (1556-60), una vasta enciclopedia un tanto desordenada dividida en seis partes; las dos primeras partes fueron publicadas en Venecia el año 1556, y las otras cuatro, póstumamente, en 1560. La primera parte es un tratado muy extenso de aritmética practica, y la segunda estudia la aritmética teórica sobre la base de la representación geométrica euclidiana; es notable en ella el desarrollo de las once primeras potencias del binomio con el triángulo de los coeficientes. La tercera, en cambio, es una exposición de geometría práctica, en la que erróneamente se identifica a Euclides, autor de los Elementos, con Euclides de Mégara, atribuyéndole la definición de la recta como línea de longitud mínima.

La cuarta parte se ocupa de la geometría especulativa, y en la quinta parte los desarrollos geométricos, primero en el plano y después en el espacio, amplían los ya contenidos en los Elementos de Euclides. La sexta parte inicia el tratado del álgebra, pero se limita a exponer las ecuaciones de segundo grado o las que son reducibles a tal categoría; el fallecimiento del autor impidió que llegase a exponer las ecuaciones de tercer grado, que son las que más interesan para la historia de las matemáticas. La obra se difundió rápidamente por Italia y fue muy conocida y apreciada también en el extranjero.

Triángulo de Tartaglia

Cuando la suma de dos términos elevamos al cuadrado vemos que la parte literal de los términos (de momento no tenemos en cuenta los coeficientes o parte numérica de los términos resultantes) sigue una ley sencilla e interesante:

Podríamos escribir también:

Recuerda que una potencia de exponente cero vale 1. Como a0 y b0 valen 1 cualquier valor por 1 no cambia el resultado.

Si te fijas bien en el resultado, los exponentes de a van decreciendo de uno en uno. Comienza en 2 y acaba en cero.

Los exponentes de b hacen lo contrario, comienzan por cero y acaban en 2.

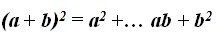
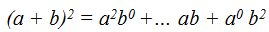
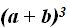Supongamos que tenemos: o el cubo de la suma de dos números, la parte literal del resultado sería teniendo en cuenta lo que acabamos de estudiar:

Los exponentes de a van decreciendo de uno en uno y los de b crecen de uno en uno. Verás, que siempre, el grado de cada término equivale al exponente al que elevamos la suma de los dos números.
Veamos el resultado de elevar a la cuarta potencia:

Observa que la suma de exponentes de la parte literal de cada término siempre será igual a la potencia a la que hemos elevado el binomio.
De ahora en adelante, omitimos los exponentes de exponente cero por valer 1. Da igual que a un número lo multipliques o no por 1, continua con el mismo número:

 Resolución de la ecuación de tercer grado

Sea una ecuación de tercer grado cualquiera, por ejemplo x³ — 5x² + 17x — 13 = 0. Su resolución, según Tartaglia y Cardano, es la siguiente: 

Se reduce a la forma X³ + pX + q = 0, mediante el cambio de variable oportuno.

En este caso X = x + 2.

La ecuación anterior se convierte en:

           X³—18X—35 = 0                    (I) 

Haciendo un nuevo cambio de variable: X = u + v, y teniendo en cuenta que:

 (u + v)³ = u³ + 3uv v (u + v) + v³, resulta:  

X³ = u³+ 3u.v(u+v)+v³ = u³+3uvX+v3X³-3uvX-(u³+v³)    (II)

Comparando las ecuaciones (I) y (II) se llega a:

3u v = 18
u³ + v³ = 35

El sistema anterior se puede resolver de la siguiente manera: 

(u³ + v³)² = 35² ==> u⁶ +2u³ v³ + v⁶ = 1225 ==> u⁶ – 2u³ v³+ 4u³ v³ + v⁶ = 1225

==> (u³—v³)²= 1225-4u³. v³ ==> (u³—v³)² = 1225—4.(18/3)³ = 1225-864 = 361 ==> u³-v³ = 19

Por tanto, el sistema queda reducido a: 

u³+v³ = 35
u³—v³ = 19

Resolviéndolo, se obtiene u = 3, y = 2. Deshaciendo los cambios de variable:

 X = u + v = 5 x = X – 2 = 3 

Por tanto, x = 3 es una raíz de la ecuación inicial de tercer grado, por lo que se puede expresar:

(x —3) (x² + 9x + 21) = 0

 

Resolviendo la ecuación de segundo grado se obtienen las otras dos soluciones. En este caso existen para ella soluciones complejas, concretamente 

x = —9/2 + 3/2 i, x = —9/2 — 3/2 i.

 He sacado la información de:

• Biografíasyvidas
• Google Imágenes
• aulafacil.com
• historiaybiografias