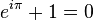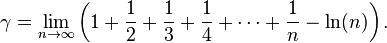EMMY NOETHER
Biografía
(Amalie Emmy Noether; Erlangen, Alemania, 1882 - Bryn Mawr, Estados
Unidos, 1935) Matemática alemana. Hija del eminente matemático
Max Noether, hubo de asistir a las clases impartidas por su
padre como oyente, dada la imposibilidad de matricularse en la
universidad por su condición
de mujer.
Finalmente fue admitida en Erlangen, donde en 1907 se doctoró con un célebre trabajo sobre los invariantes; sus estudios en este
campo fueron inmediatamente apreciados por Albert
Einstein, que se serviría de sus aportaciones para la formulación de algunos aspectos de la relatividad general. David
Hilbert la invitó a impartir
una serie de conferencias en Gotinga, pero la oposición de parte
del profesorado únicamente le permitió acceder a un puesto no oficial
de profesora
asociada.
La ascensión de los nazis al poder forzó su
exilio en Estados Unidos; se estableció en Nueva Jersey, donde prosiguió
con sus trabajos en el Instituto de Estudios Avanzados de Princeton y
como profesora en Bryn Mawr.
Las investigaciones de Emmy Noether ejercieron
una amplia y profunda influencia en el desarrollo del álgebra moderna y
de la topología. Noether estudió los conceptos matemáticos de anillo e
ideal, unificó en un solo cuerpo teórico las diferentes aproximaciones
anteriores y reformuló en el marco del mismo la teoría de los
invariantes algebraicos; dotó de ese modo de un nuevo enfoque a la
geometría algebraica.
Obra
Primera época (1908-19)
Teoría de la invariante algebraica
La teoría de los invariantes trata de las expresiones que permanecen constantes (invariantes) bajo grupos de transformaciones.
El ejemplo arquetípico de una invariante es el discriminante B2 − 4AC de una forma binaria cuadrática de Ax2 + Bxy + Cy2. A esta se le llama invariante porque no cambia por substituciones lineales x→ax + by, y→cx + dy con determinante ad − bc = 1. Estas substituciones forman el grupo lineal especial SL2. (No hay invariantes bajo el grupo lineal general de todas las transformaciones lineales invertibles porque estas transformaciones pueden ser multiplicación por un factor escalar. Para remediarlo, la teoría clásica de los invariantes también considera invariantes relativas, que eran formas de invariancia salvo un factor escalar).
Una de las principales metas de la teoría de los invariantes es resolver el "problema de base finita". La suma o producto de dos invariantes cualesquiera es un invariante, y el problema de la base finita planteaba si era posible obtener todos los invariantes comenzando por una lista finita de invariantes, llamados generadores, y después añadir o multiplicar los generadores entre sí.
Teoría de Galois
La teoría de Galois trata de las transformaciones de cuerpos numéricos que permutan las raíces de una ecuación.
Ya que el grupo de Galois no cambia el cuerpo base, deja los coeficientes del polinomio inalterados, de modo que debe también dejar inalterado el conjunto de todas las raíces. Sin embargo, cada raíz puede transformarse en otra raíz, de modo que la transformación determina una permutación de n raíces entre sí mismas.
Noether publicó un artículo de gran importancia sobre el problema inverso de Galois. En lugar de determinar el grupo de Galois de transformaciones de un cuerpo dado y su extensión, Noether se preguntó si, dado un cuerpo y un grupo, siempre es posible encontrar una extensión del cuerpo que tenga al grupo dado como su grupo de Galois. Redujo esto al llamado problema de Noether, que pregunta si el cuerpo fijo de un subrupo G del grupo de permutaciones Sn actuando sobre el cuerpo k(x1, ... , xn) es siempre una extensión trascendente pura del cuerpo k.
Segunda época (1920-26)
Condiciones ascendentes y descendentes de cadena
Se dice que una sucesión de subconjuntos no vacíos A1, A2, A3, etc. de un conjunto S es estrictamente ascendente si cada uno es un subconjunto del siguiente.
La condición de cadena ascendente requiere que estas sucesiones se descompongan después de un número finito de pasos.
Las condiciones ascendentes y descendentes de cadena son generales, es
decir, se pueden aplicar a muchos tipos distintos de objetos
matemáticos, y a primera vista no parecen muy potentes. Sin embargo
Noether mostró cómo explotar esas condiciones para obtener las máximas
ventajas.
Muchos tipos de objetos en un álgebra abstracta pueden satisfacer las condiciones de cadena, y habitualmente si satisfacen una condición ascendente de cadena se llaman noetherianos en su honor. Por definición, un anillo noetheriano satisface una condición ascendente de cadena en sus ideales izquierdo y derecho, mientras que un grupo noetheriano se define como un grupo en el que toda cadena estrictamente ascendente de subgrupos es finita. Un módulo noetheriano es un módulo en el que toda cadena estrictamente ascendente de submódulos se descompone después de un número finito. Un espacio noetheriano es un espacio topológico en el que toda cadena estrictamente ascendente de subespacios abiertos se descompone después de un número finito de términos.
Otra aplicación de estas condiciones de cadena es la inducción noetheriana —también conocida como orden bien fundamentado— que es una generalización de la inducción matemática.
Frecuentemente se usa para reducir proposiciones generales sobre
colecciones de objetos a proposiciones sobre objetos en particular de
esa colección.
Teoría de la eliminación
Noether aplicó su teoría de ideales a la teoría de la eliminación mostrando que los teoremas fundamentales de la factorización de polinomios podían trasladarse directamente. Tradicionalmente, la teoría de la eliminación se ocupa de la
eliminación de una o más variables de un sistema de ecuaciones
polinómicas, habitualmente mediante el método de las resultantes. Para ilustrar este punto, un sistema de ecuaciones frecuentemente puede escribirse como el producto de una matriz M (cuyos elementos son los coeficientes) por un vector v (cuyas componentes son las potencias sucesivas de x) que se iguala al vector cero, M•v = 0. Como consecuencia, el determinante de la matriz M debe ser igual a cero, lo que da lugar a una nueva ecuación en la que la variable x ha sido eliminada.
Tercera época (1927-35)
Números hipercomplejos y teoría de la representación
Se habían llevado a cabo muchos trabajos sobre los números hipercomplejos y representaciones de grupo a principios del siglo XX,
pero seguían siendo dispares. Noether unificó los resultados y dio la
primera representación general de la teoría de grupos y álgebras. En resumen, Noether subsumió la teoría estructural del álgebra asociativa
y de la representación de grupos en una única teoría aritmética de
módulos e ideales que satisfacen las condiciones ascendentes de cadena.
Este único trabajo de Noether es de fundamental importancia para el
desarrollo del álgebra moderna.
Álgebra no conmutativa
Un artículo muy influyente publicado por Noether, Helmut Hasse, y Richard Brauer trató de las álgebras de división, que son aquellos sistemas algebraicos en los que es posible la división. Probaron dos teoremas importantes; un teorema local-global que afirma que si un álgebra de división finita dimensional central sobre un cuerpo numérico algebraico se descompone localmente en cualquier elemento, entonces se descompone también globalmente (con lo que es trivial), y de esto dedujeron su teorema principal (Hauptsatz): todo álgebra de división central finito-dimensional sobre un cuerpo numérico algebraico F se descompone sobre una extensión cíclica ciclotómica. Estos teoremas permiten clasificar todas las álgebras de división finito dimensionales y centrales sobre un cuerpo numérico dado. Un artículo posterior mostró, como un caso especial de un teorema más general, que todos los subcuerpos maximales de un álgebra de división D son cuerpos de descomposición. Este artículo también contiene el teorema de Skolem-Noether que afirma que dos inclusiones de una extensión de un cuerpo K en un álgebra simple central finito-dimensional sobre K, son conjugados. El teorema de Brauer-Noether ofrece una caracterización de los cuerpos de descomposición de un álgebra de división central sobre un cuerpo.
He sacado la información de:
- biografiasyvidas
- Google Imágenes
- Wikipedia




 ,
,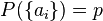 .
.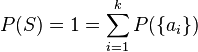 entonces
entonces  .
. entonces
entonces 
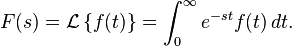

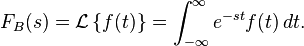
 es llamado el operador de la transformada de Laplace.
es llamado el operador de la transformada de Laplace.






 para hacer referencia a la unidad imaginaria. El uso de la letra griega
para hacer referencia a la unidad imaginaria. El uso de la letra griega  como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función
como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función 

 es exactamente 1. Es más, es el número real tal que la función
es exactamente 1. Es más, es el número real tal que la función 
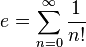
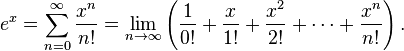
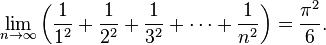


 =
=  ), lo que se conoce como la identidad de Euler:
), lo que se conoce como la identidad de Euler: